Finding perpendicular lines and vectors
In this blog post, I will demostrate some examples of using linear algebra and Python to find perpendicular lines and vectors, as well as parallel lines at certain distance (which piggy-backs on the perpendicularity information).
We will first import NumPy and Matplotlib, as well as some helper functions previously described in the earlier blog post about homogeneous vectors.
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.patches import Polygon
from helpers import e2h, prepare_canvas, plot_line, plot_vector
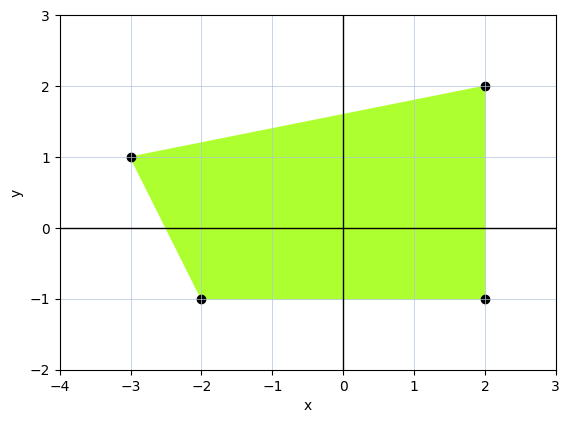
Let’s start with a polygon made up from a few line segments, with one purely horizontal and one purely vertical:
polygon_points = np.array([
[-3, 1],
[2, 2],
[2, -1],
[-2, -1]
], dtype=float)
The points, as they listed, define the top, right, bottom and left sides respectively. Let’s visualize the polygon:
X_RANGE = (-4, 3)
Y_RANGE = (-2, 3)
def add_polygon_to_ax(ax, polygon_points):
ax.add_patch(Polygon(polygon_points, color='greenyellow'))
ax.scatter(polygon_points[:, 0], polygon_points[:, 1], color='black')
def viz_polygon(polygon_points):
_, ax = plt.subplots()
prepare_canvas(ax, X_RANGE, Y_RANGE)
add_polygon_to_ax(ax, polygon_points)
plt.show()
viz_polygon(polygon_points)
As described in this post, given two points expressed as homogeneous vectors, we can obtain a homogeneous vector representaion of the line by doing cross-product. We can code it up:
def create_line_vector(p0, p1):
return np.cross(e2h(p0), e2h(p1))
Let’s then create a function for getting pairs of points representing sides of a polygon:
def get_polygon_sides_as_point_pairs(polygon_points):
pairs = []
n = len(polygon_points)
for i in range(n):
a = polygon_points[i]
b = polygon_points[(i + 1) % n]
pairs.append((a, b))
return pairs
We can then use get_polygon_sides_as_point_pairs and create_line_vector to create a list of line vectors for each side a of a polygon:
def polygon_sides_to_line_vectors(polygon_points):
vectors = []
for a, b in get_polygon_sides_as_point_pairs(polygon_points):
vectors.append(create_line_vector(a, b))
return vectors
Let’s put all of this in action with our polygon points:
line_vectors = polygon_sides_to_line_vectors(polygon_points)
for line_vec in line_vectors:
print(line_vec)
[-1. 5. -8.]
[ 3. 0. -6.]
[ 0. -4. -4.]
[-2. -1. -5.]
As a reminder, a line vector $(a, b, c)^T$ corresponds to the following form of line equation:
$$ a x + b y + c = 0 $$
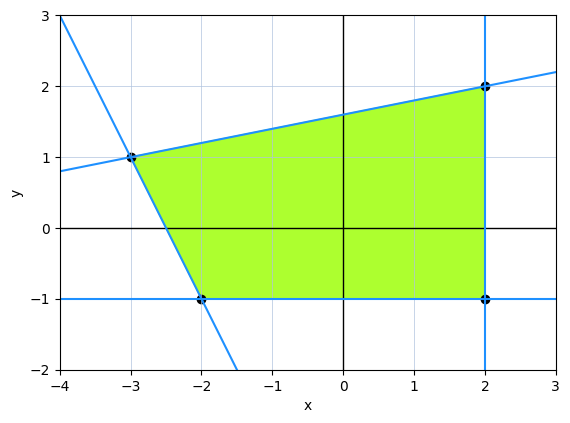
You may observe that the second and the third line vectors above contain 0 in the second and the first place respectively. This correspond to our vertical and hortizontal line. We can now inspect all the lines visually:
def viz_polygon_with_lines(polygon_points, line_vectors):
_, ax = plt.subplots()
prepare_canvas(ax, X_RANGE, Y_RANGE)
add_polygon_to_ax(ax, polygon_points)
for line_vec in line_vectors:
plot_line(ax, line_vec, linestyle='-', color='dodgerblue')
plt.show()
viz_polygon_with_lines(polygon_points, line_vectors)
Given the line vectors above, we can now find the correspding perpendicular lines.
A line perpendicular to $a x + b y + c = 0$ has the following form:
$$ b x - a y + c’ = 0 $$
where the constant $c’$ can be arbitrary, depending on which point this line should pass through.
We can create exactly such function, which will find the perpendicular line vector for the given line vector and the point for the perpendicular line to pass through:
def perpendicular_line_through_point(line_vector, point):
a, b, _ = line_vector
x, y = point
c_new = a * y - b * x
return np.array([b, -a, c_new])
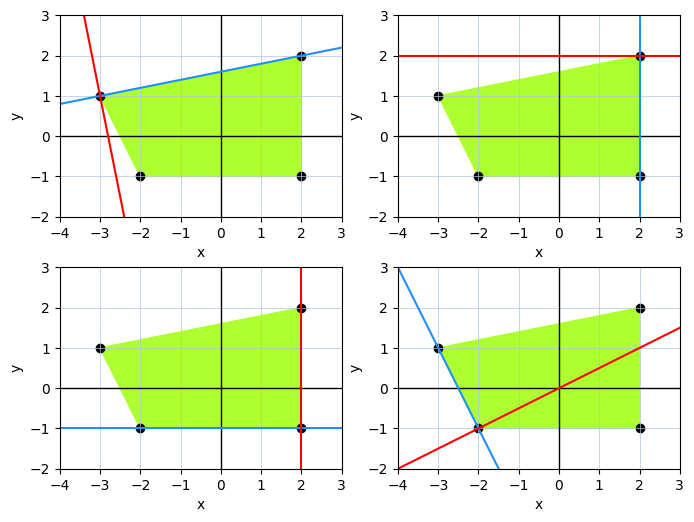
For our example it might be interesting to use the first point of each polygon segment as the through-point. Let’s see how it all works:
def viz_perpendicular_lines(polygon_points, line_vectors):
def show_two_perpendicular_lines(ax, polygon_points, line_vec, perp_line_vec):
add_polygon_to_ax(ax, polygon_points)
plot_line(ax, line_vec, linestyle='-', color='dodgerblue')
plot_line(ax, perp_line_vec, linestyle='-', color='red')
_, axes_grid = plt.subplots(2, 2, figsize=(8, 6))
axes = axes_grid.flatten()
for ax in axes:
prepare_canvas(ax, X_RANGE, Y_RANGE)
for ax, point, line_vec in zip(axes, polygon_points, line_vectors):
perp_line_vec = perpendicular_line_through_point(line_vec, point)
show_two_perpendicular_lines(ax, polygon_points, line_vec, perp_line_vec)
plt.show()
viz_perpendicular_lines(polygon_points, line_vectors)
What if we want to find parallel lines at certain distance from the original line? For this, we can piggy-back on the idea of perpendicularity: if we know the perpendicular direction, we can find a point at certain distance in this direction.
The first step is to find the perpendicular direction. It is natural to use a vector for it, and the straightforward way to get it is to simply rotate the original vector. With our polygon data, we already have the points, so we can use them as anchors, and the “original vectors” will be vectors obtained from each point pair of a polygon side.
Let’s define a function that finds a vector of the desired length perpendicular to the original vector by doing a simple rotation by $\pi / 2$:
def perpendicular_to(v, length=1.):
theta = np.pi / 2
c = np.cos(theta)
s = np.sin(theta)
rot_matrix = np.array([[c, -s], [s, c]])
v_rotated = rot_matrix @ v
return (v_rotated / np.linalg.norm(v_rotated)) * length
Each pair of our polygon points forms a vector, and we can find the perpendicular directions for each of them using the function above. The following example finds perpendicular vectors of length 1:
def viz_polygon_with_vectors(polygon_points):
_, ax = plt.subplots()
prepare_canvas(ax, X_RANGE, Y_RANGE)
add_polygon_to_ax(ax, polygon_points)
for a, b in get_polygon_sides_as_point_pairs(polygon_points):
v = b - a
v_perp = perpendicular_to(v, length=1.)
plot_vector(v, origin=a)
plot_vector(v_perp, origin=a+v, color='blue')
plt.show()
viz_polygon_with_vectors(polygon_points)

If we have a line vector $(a, b, c)^T$ and we want to find a parallel line to it at certain distance, we’ll reuse $a$ and $b$ (since they define the slope, which will be the same), but we need to find the intercept component $c’$ that would correspond to the line passing through a certain point. We do this with the function below:
def line_through_point(base_line_vector, point):
a, b, _ = base_line_vector
x, y = point
c = - a * x - b * y
return np.array([a, b, c])
The point through which our parallel line will pass is conveniently available as the “tip” of the perpendicular direction vector we obtained earlier. In the example below, we find parallel lines to each side of the polygon at the distance of 0.7:
def viz_parallel_lines(polygon_points):
_, ax = plt.subplots()
prepare_canvas(ax, X_RANGE, Y_RANGE)
add_polygon_to_ax(ax, polygon_points)
for a, b in get_polygon_sides_as_point_pairs(polygon_points):
v = b - a
v_perp = perpendicular_to(v, length=0.7)
p = b + v_perp
line_original = create_line_vector(a, b)
line_parallel = line_through_point(line_original, p)
plot_vector(v, origin=a)
plot_vector(v_perp, origin=a+v, color='blue')
plot_line(ax, line_parallel, linestyle='-', color='tab:green')
ax.scatter((p[0], ), (p[1], ), color='tab:green')
plt.show()
viz_parallel_lines(polygon_points)

